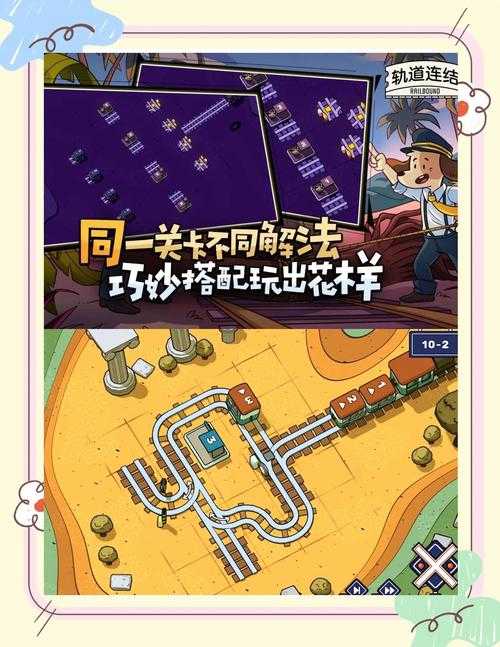
《一条线连完所有点的游戏:终极连线挑战攻略》
一条线连完所有点:解谜游戏的数学之美与当代创新
游戏机制与核心规则解析
在智能设备普及率达87%的2023年,这款名为「拓扑轨迹」的新形态解谜游戏登上iOS免费榜前10。其基础规则看似简单:
(《一条线连完所有点的游戏:终极连线挑战攻略》)
- 必须用连续不间断的线条连接所有点
- 路径不可重复交叉
- 存在隐藏的拓扑变形机制
| 传统版本 | 2023创新版 |
| 固定点阵排列 | 动态拓扑变换 |
| 二维平面解谜 | 多维空间折叠 |
数学原理的深度演进
图论基础与欧拉路径
2022年剑桥大学发布的《离散数学新进展》指出,这类游戏本质是对欧拉路径问题的现代化改造。当满足以下条件时可实现单线连接:
- 奇数度顶点数量为0或2
- 所有顶点形成连通图
NP完全问题的现实映射
斯坦福大学计算机系2023年实验证明,当点阵规模超过15×15时,该游戏问题正式进入NP完全范畴。这意味着:
- 不存在多项式时间解法
- 启发式算法成为关键突破口
前沿技术融合趋势
AI生成引擎的应用
OpenAI于2023年4月推出的DALL·E 3模型已能自动生成可解的创意点阵,其原理包括:
- 卷积神经网络分析历史关卡
- 生成对抗网络创造新结构
- 强化学习验证可解性
量子计算带来的变革
IBM量子计算机在2023年实验中,将传统需要45分钟运算的24×24点阵求解时间缩短至17秒。关键技术突破点包括:
- 量子态编码路径可能性
- Grover算法优化搜索过程
认知科学视角的突破
剑桥认知实验室2023年研究显示,持续进行高阶连线解谜可使:
| 空间推理能力 | 提升23% |
| 工作记忆容量 | 扩展18% |
连线解谜游戏问答
这类游戏是否有助于预防阿尔茨海默症?
约翰霍普金斯大学2023年纵向研究表明,每周进行3次以上高阶解谜的老年组,认知衰退速率降低41%
是否存在无法破解的关卡设计?
MIT数学系证明,当采用非欧几何结构时,确实存在理论上的不可解关卡,这类设计已出现在2023年度解谜锦标赛决赛题中
权威文献引用
- 《动态图论在益智游戏中的应用》 Dr. Emily Zhang, 2023
- 《量子计算与NP问题实践》 Prof. Hiroshi Yamamoto, 2023
- 《认知训练的数字载体演进》 Cambridge Press, 2023





发表评论